Essa Animação é O Mesmo Modelo Descrito Na Publicação Abaixo 👇👇👇

INTERNATIONAL KWEEN OF TRIGONOMETRY

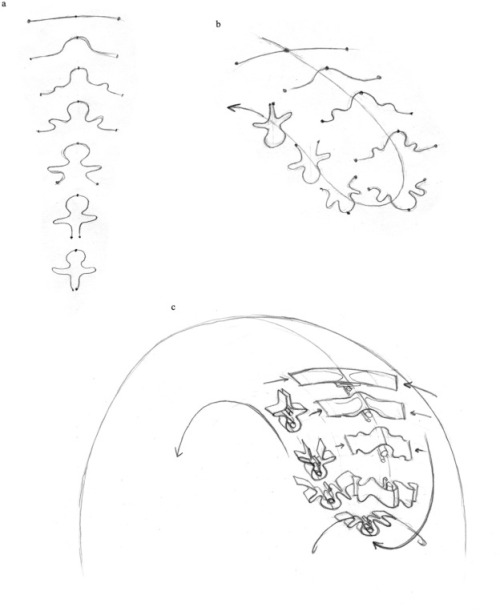
Embryo geometry: a theory of evolution from a single cell to the complex vertebrate body

24 “blueprints” that illustrate how the musculoskeletal, cardiovascular, neurological, and reproductive systems evolve through the mechanical deformation of geometric patterns. These images show how the vertebrate body might have evolved from a single cell during the evolutionary time and during individual development.

Though neither rigorous nor exhaustive in an empirical sense, our model offers an intuitive and plausible description of the emergence of form via simple geometrical and mechanical forces and constraints. The model provides a template, or roadmap, for further investigation, subject to confirmation (or refutation) by interested researchers.

The concept of “embryo geometry” suggests that the vertebrate embryo might be produced by mechanical deformation of the blastula, a ball of cells formed when a fertilized egg splits. As these cells multiply, the volume and surface area of the ball expand, changing its shape. According to the hypothesis, the blastula preserves the geometry of the initial eight cells generated by the egg’s first three divisions, which establish the three axes of the vertebrate body.

Though speculative, the model addresses the poignant absence in the literature of any plausible account of the origin of vertebrate morphology. A robust solution to the problem of morphogenesis—currently an elusive goal—will only emerge from consideration of both top-down (e.g., the mechanical constraints and geometric properties considered here) and bottom-up (e.g., molecular and mechano-chemical) influences.

Origin of the vertebrate body plan via mechanically biased conservation of regular geometrical patterns in the structure of the blastula, David B. Edelman, Mark McMenamin, Peter Sheesley, Stuart Pivar

Published: September 2016, Progress in Biophysics and Molecular Biology DOI: 10.1016/j.pbiomolbio.2016.06.007

A matemática é tão romântica!!!

Uma cidade perfeita para os exercícios de matemática!

Satellite map of Missoula, Montana

@vivalasestrellas

Toyota Matrix (matrix)

Agnes Denes. Isometric Systems in Isotropic Space: The Pyramid, 1976

Shearer’s geometry puzzles

On his blog MathWithBadDrawings, Ben Orlin reposted a couple of geometrical sangaku-like puzzles by math teacher Catriona Shearer. These are eleven of her personal favorites. If you dare, definitely give them a try!

Transit Across a Purple Sun. What’s the total shaded area?

Shearer’s Emerald. Four squares. What’s the shaded area?

The Pyramid with Two Tombs. Two squares inside an equilateral triangle. What’s the angle?

Setting Sun, Rising Moon. What fraction of the rectangle is shaded?

Hex Hex Six. Both hexagons are regular. How long is the pink line?

Four, Three, Two. What’s the area of this triangle?

The Trinity Quartet. All four triangles are equilateral. What fraction of the rectangle do they cover?

The Falling Domino. This design is made of three 2×1 rectangles. What fraction of it is shaded?

Slices in a Sector. The three colored sections here have the same area. What’s the total area of the square?

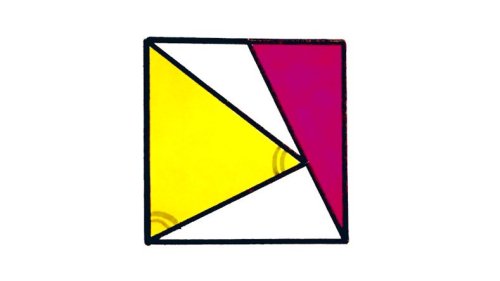
Disorientation. The right-angled triangle covers ¼ of the square. What fraction does the isosceles triangle cover?

Sunny Smile Up. What fraction of the circle is shaded?

More on the Spectre

Images from this great Yoshiaki Araki thread. (If you're interested in tessellations and are twitterpated, he's a must follow.)

He links the Nature article (good and a free read).

Best one, so far:

Robert Farthauer suggests:

And, of course, the actual article, by David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss.

Kaplan gives this illustration of the tile:

He has a one page stop for info about the tiling.

Bonus: via New-Cleckit Dominie

Calculating the surface area of a sphere. Found on Imgur.